扫雷的逻辑

理论永远只能支持一部分的答案，而不能给你全部的答案。

——廖伟青 (Id: 208)

✍文章痕迹

写作时间线

10-11 13:53

创建文章，准备写成益智游戏推荐。

10-12 20:45

了解很多东西，开始重新规划文章

10-13 9:32

这游戏复杂地令人咂舌，已经不是基本的非齐次线性方程组求解的问题了，NP与P问题，˶⍤⃝˶꒳ᵒ꒳ᵎᵎᵎ，是我没有接触的内容。这东西写成一篇论文也不为过。对啊，咱家再仔细研究研究，可以把它写篇10000字左右的小论文/优秀博文啊！噫，真不错，这个点子真NICE!

10-14～10-16

练习扫雷，创造了个人最佳记录

10-17

1. 试图用行列式，矩阵来解释。
2. 明确了定义
3. 打破纪录，更新截图
4. 绘制封面
5. 添加了电路 [^6]

10-28 烂尾

过于复杂，灵感枯竭，思路不接，时间不够…所以决定烂尾了

---

绪论

一开始我压根没想到这篇文章有这么复杂，压根儿没想到扫雷的水这么深。

你可知道，在这人世间，有一种神奇无比的游戏：

有人以它为原型设计了感冒药的广告 ^1
有的人把它做成了逻辑电路，并证明了它是NP完全的 ^[1]
有的人从游戏中得到灵感，设计了新型的核酸检测交叉感染检测算法 ^[2]
有人把游戏规则进一步抽象，构建了隐私网络效应模型 ^[3]
有人借用围棋的策略，破了游戏里的高分记录 ^[4]
有人从中体会到了人生
…

作出了选择，无论是什么结果，你都必须一个人去承受。
对的选择并不能使你一路到达目标，但错的选择你则会全盘皆输。
你永远不会有一步达到目标的可能，但好的开始会使你走得更好。
在前进方向面临多重选择的时候，选择前景更开阔的道路。
做出选择往往是痛苦的，可优柔寡断将可能使你失去本该属于你的机会。

这就是扫雷游戏(Minesweeper)，一款始创于windows系统，经久不衰，极其耐玩的益智游戏。

玩法很简单

1. 目标：排出所有的雷
2. 规则：数字代表周围雷的数量
3. 操作：点击打开空格，显示空格的状态，(标记可以辅助记录雷的分布)，一直打开无雷的空格知道找到所有的雷。

初等代数解读

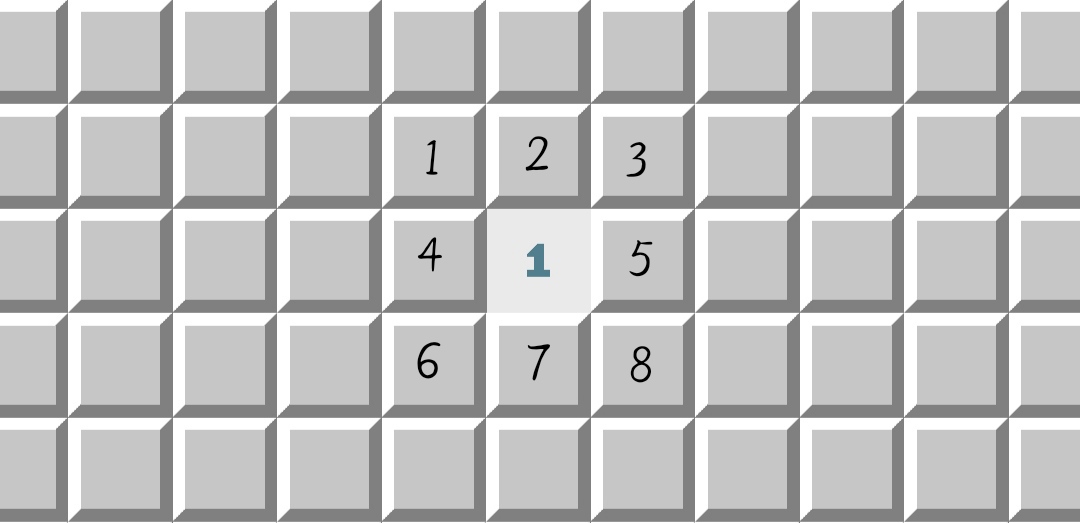
如果我在雷区中间上随便点了一点，碰巧没有踩到雷，那么就会出现如上图所示的结果。当然，中间的数字不仅仅会是1，也可能是0、2、3、4、5、6、7、8、9中的一个。
为了方便说明，我们定义如下几个概念

• 排雷：表示点击未定块确定其状态的动作。
• 标记(Flag)：表示在未定块上放置小红旗的动作。
• 雷(Mine)：表示未定块的状态是雷。
• 定数(Determined Number)：如上图中1所示的拍雷过后的一个非雷的确定方块上的值称为定数，代表除自身外，其他周围八个块上雷的数量。
• 未定块(Block)：代表没有排过雷的不确定方块，显然，未定块的状态可以是一个定数也可以是雷{

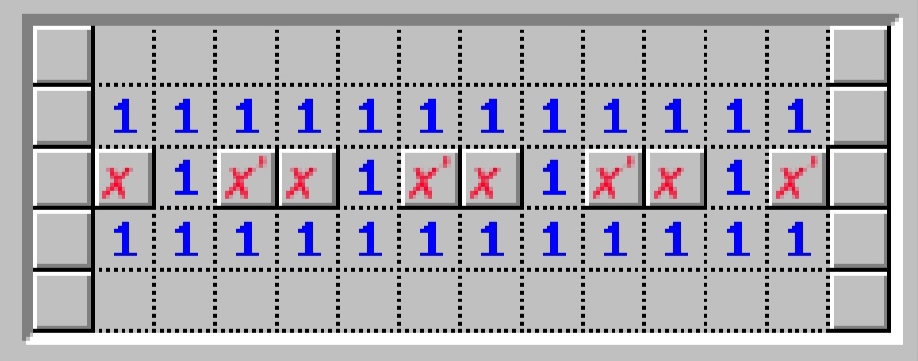
我们先看以定数1为中心的这个九宫格：我们从左往右、从上到下把这八个未定块依次表示为$x_1,x_2\dots x_8$。那么可以做成这样的一个方程：

$$x_1+x_2+x_3+x_4+x_5+x_6+x_7+x_8=1$$

显然$x_i$的值可以分成两层：

1. 雷层。要么是雷，要么不是雷。在这一层$x_i$只能取$0$(代表没有雷)或$1$(代表雷)
2. 数层。一块儿最多周围有八个块儿，八个雷，故$x_i$在定数层可以取${0,1,2,3,4,5,6,7,8}$

我们进一步把$x_i$写成为$x_{(m,n)}$的形式：其中m为雷层，n为数层。比如：$x_{(0,0)}$代表非雷且定数为0的块(九格全非雷) ，$x_{(0,3)}$代表非雷且定数为3的块，$x_{(0,8)}$代表非雷且定数为8的块等等。当未定块是雷的时候，游戏中一般不会显示出来定数层，但不代表不存在，我们进一步抽象，比如用$x_{(1,3)}$来表示雷且数层为3的块(周围有三个雷)，$x_{(1,8)}$表示雷且定数为8的块(九格全雷)
等。这样就可以建立一个简单的数学模型：九个2×1的矩阵组成的满足一定关系的大矩阵

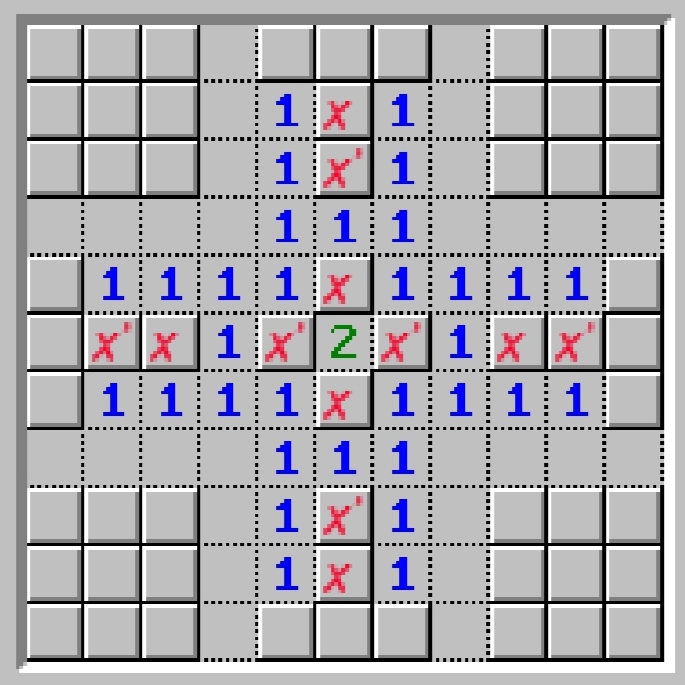
但受到游戏规则所限，我们秉不关心当m=1时n的值，所以再把模型简化下。有两个解的情况:比如下图黑框框里的6×2=12个块，虽然六个块都确定了，但也只是六个常数项，配上六个未知数。

矩阵的意义

真谛

关于开源工作者、Mod开发者的思考

劳动被剥削，开源软件SSH等，

MOD以泰拉瑞亚为例，所有的收入都归于开发者，虽然他们支持了开源软件，但也不能掩盖其资本家的本性。

以开源游戏：迷你工厂为例，不存在收入，只有捐赠，但其宿主获得收益

软件推荐

Windows

系统自带

Linux

随便找个就好

安卓

推荐Material Design的AntiMine(扫雷)，自定义选项很多，各种主题，配乐也很舒服。

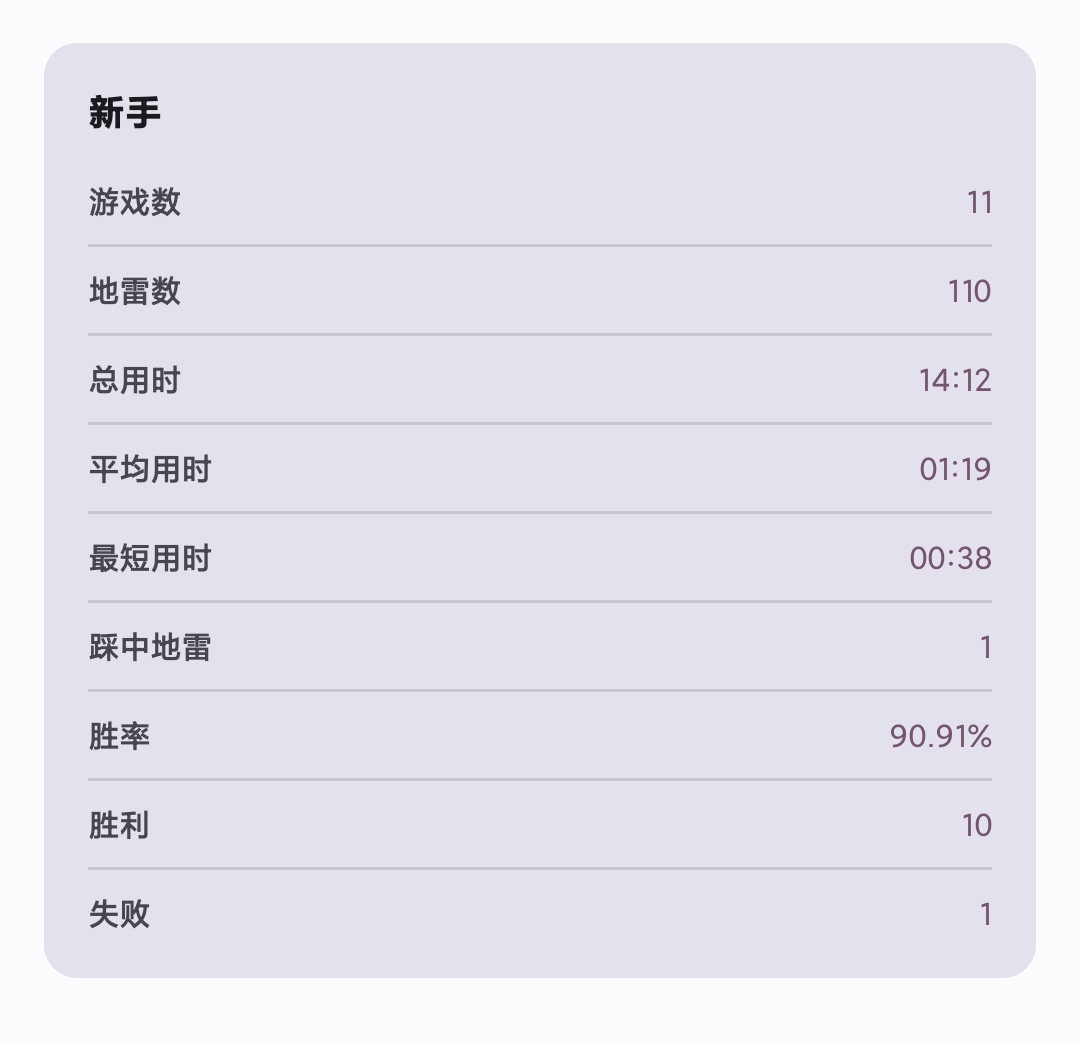
个人记录

10-17日下午 四点到五点做完2010年数二真题后来了手感，破了两天前的新手、中等、专家模式的记录

扫雷看似简单，但实际上暗藏玄机。最近做了一些线性代数题目，按照我的观察：扫雷似乎可以理解为线性方程组求解的问题。

封面背后

以2020年某晴朗冬日的下午，在新大南校区操场上拍摄的足球网为基础制作。

---

1. https://web.mat.bham.ac.uk/R.W.Kaye/minesw/ordmsw.htm ↩︎

2. 张海龙,牟小会,王萍,滕敏.用“扫雷游戏”原理标识新型冠状病毒核酸检测中的可能交叉污染孔[J].检验医学与临床,2023,20(13):1954-1957 ↩︎

3. 李佳欣.基于扫雷游戏的隐私网络效应模拟[J].科技风,2018(18):64-64 ↩︎

4. http://saolei.wang/BBS/Title.asp?Id=22422 ↩︎