真实世界 | 子虚栈

未完待续。
——片间字幕

✍文章痕迹

写作时间线

2024-9-30

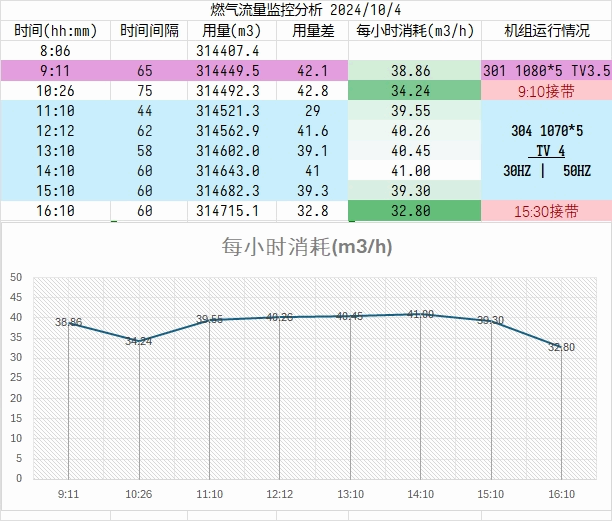
上月产线燃气用量异常，本月开始追踪燃气耗量

每小时抄表一次，收集数据
拍摄快照。盲目收集所有变量，无思路，

2024-10-15

更换数据数据模板：利用Excel函数自动计算
找到思路：F提出TV与耗量的经验关系：TV越大，耗量越多

2024-10-16

与收集数据做对比，确定经验规律有效，继续抄表收集数据

2024-10-21

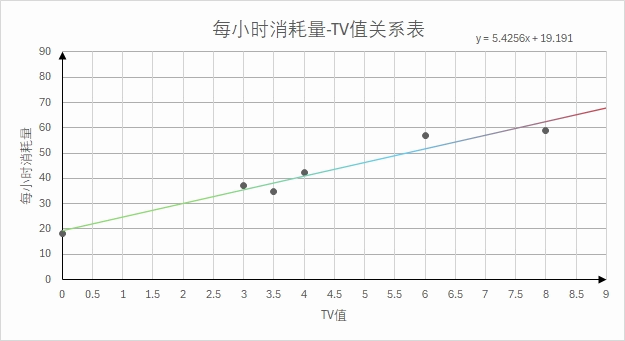
总结出线性经验公式：燃气消耗量=5.4256 X TV值+19.191——可保证误差在5%以内。但当TV大于6时，公式误差最大增大到了15。
继续收集数据，抄表频率稳定为早上八点

TV	估计每小时消耗量
0	19.191
1	24.6166
1.5	27.3294
2	30.0422
2.5	32.755
3	35.4678
3.5	38.1806
4	40.8934
4.5	43.6062
5	46.319
5.5	49.0318
6	51.7446
6.5	54.4574
7	57.1702
7.5	59.883
8	62.5958
8.5	65.3086
9	68.0214

2024-10-23

整理数据，利用二次插值、指数函数进行拟合，并与抄表数据进行验证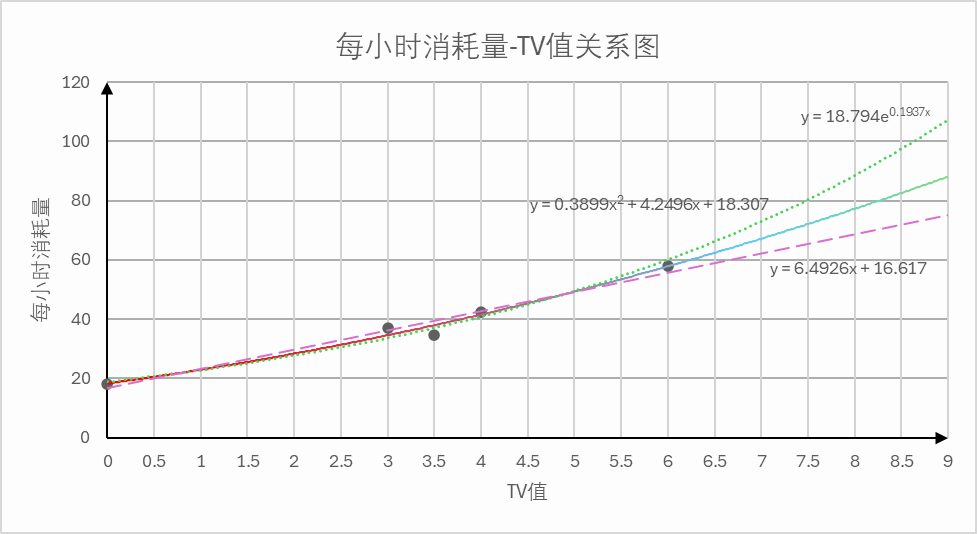

2024-10-21

问题

Q产线运行时需要消耗燃气进行加热来保持工艺温度，经观察发现——产线的工艺参数TV(x)与每小时燃气耗量(y)之间存在正相关性，现根据以下收集数据来确定某函数f(x)使y=f(x)，误差在4%以内。

经验规律

经过有针对性地统计观察得到如下三组数据：

TV	每小时燃气耗量
0	18.160
3	37.100
3.5	34.700
4	42.255
6	58.000

可以看出，数据之间存在较大的正相关性——TV越大，每小时燃气耗量越大。现通过三种方法对其进行拟合:

得到三种不同的结果：

${y=6.4926 x+16.617}$
$y=0.3899x^2+4.2496 x +18.307$
$y=18.794e^{0.1937x}$

经验规律的验证

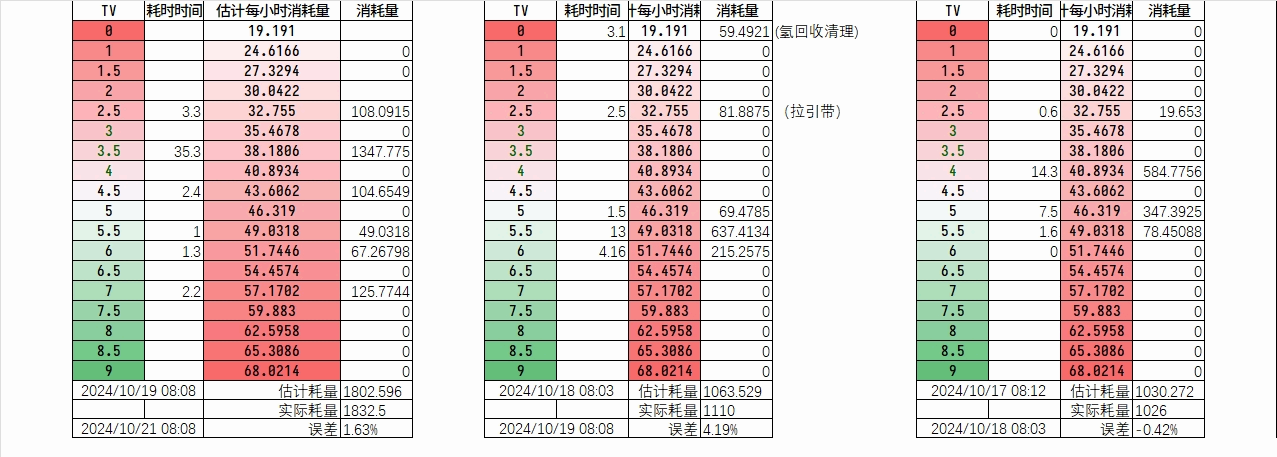
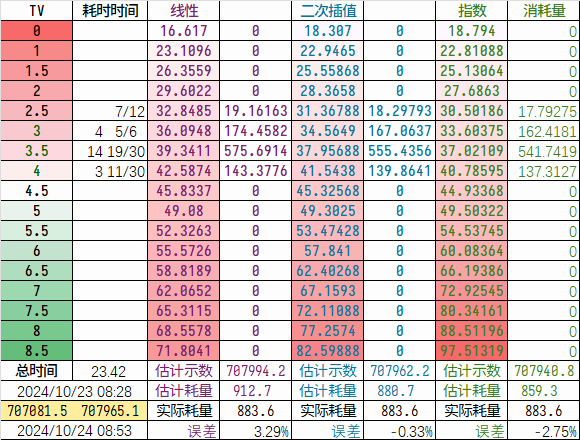
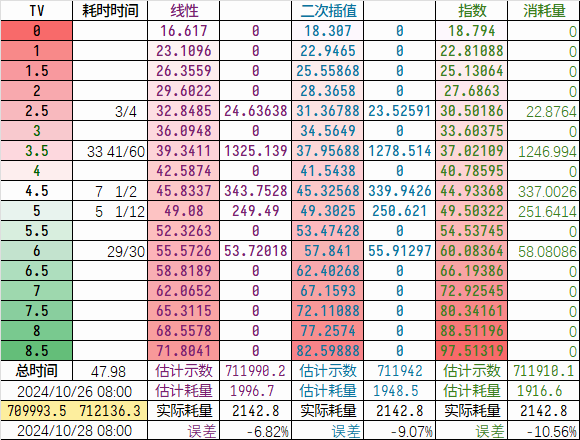
为了验证规律的准确性，通过收集每日TV值及其运行时间，以及燃气耗量，来进行验证，以2024.10.23为例，可以看出用经验规律拟合得到的预测结果误差在4%以内。

但并不是每次都可以很好预测，如2024.10.26-28，其预测误差甚至达到了11%，这是不可接受的，因而我们需要更加准确的方法来进行预测。

迭代法

迭代法，是一种数值计算方法，适用于大量数据近似解的求取，由于其初始值估测的特点，可以很好满足目前情形，特采用此方法进行更精确对应关系的求解。

迭代法的基本步骤：

求解 $Ax=b$ ，给定初始猜测 $x^{(0)}$
精确误差 $e^{(0)}=A^{-1}b-x^{(0)}$ ，残差 $r^{(0)}=b-Ax^{(0)}$ （可得到 $r^{(0)}=Ae^{(0)}$ ）
解 $Mz^{(0)}=r^{(0)}$ ，求得 $z^{(0)}$
对 $k=1,2,3,\cdots,$ 令 $x^{(k)}=x^{(k-1)}+z^{(k-1)}$ ，解出 $x^{(k)}$
计算新残差 $r^{(k)}=b-Ax^{(k)}$
解 $Mz^{(k)}=r^{(k)}$ ，求得 $z^{(k)}$

对于预优矩阵 $M$ 选择的不同，有三种迭代方式：

M取A的对角线矩阵 $D$
M取A的下三角矩阵 $-L$
M取 $\omega^{-1}D-L$ （ $\omega$ 为加速收敛系数）

#------------------初始猜测x0--------------
TV_seq = seq(2.5,6, by=0.5) # 定义TV值所在区间
x_0_1 <- cbind(TV_seq*6.4926+16.617) # 线性
x_0_2 <- TV_seq^2*0.3899+4.2496*TV_seq+18.307 #二次插值
x_0_3 <- 18.794*exp(0.1937*TV_seq) #对数插值

# 输入统计的每天TV值时间占比与消耗量的矩阵
Time_cost <- matrix(
  c(39/47, 0, 7+1/6, 6+7/60, 3+5/6, 4+5/6, 0, 9/10, 1078.6,
        0, 0, 5+1/3, 0, 7+2/3, 1+1/3, 0, 10+1/3, 1318.5,
        2/3, 0, 0, 14+1/3, 0, 7+1/2, 1+2/3, 0, 1026,
        7/12, 4+5/6, 14+19/30, 3+11/30, 0, 0, 0, 0, 833.6,
        2+1/6, 3, 11+37/60, 0, 3+1/3, 0, 3+7/12, 0, 1022.9,
        0, 0, 8+19/60, 14+19/20, 0, 0, 0, 0, 1005.5,
        3/4, 0, 33+41/60, 0, 7.5, 5+1/12, 0, 29/30, 2142.8,
        2, 0, 1, 3+11/12, 10, 1+29/30, 0, 1.5, 1000),
    ncol=9,byrow=TRUE
)

# 最后一列是每日消耗量，提取到变量y
Cost <- Time_cost[, 9]  
# 前八列是时间数据，提取到变量x
Time <- Time_cost[, 1:8]

#----------拟合计算-----------
print(max(Mod(eigen(Time)$val))) #求矩阵复数特征值的模的最大值

solve(diag(diag(Time)),r_0_1)
solve(triu(Time),r_0_1)
solve(tril(Time),r_0_1)