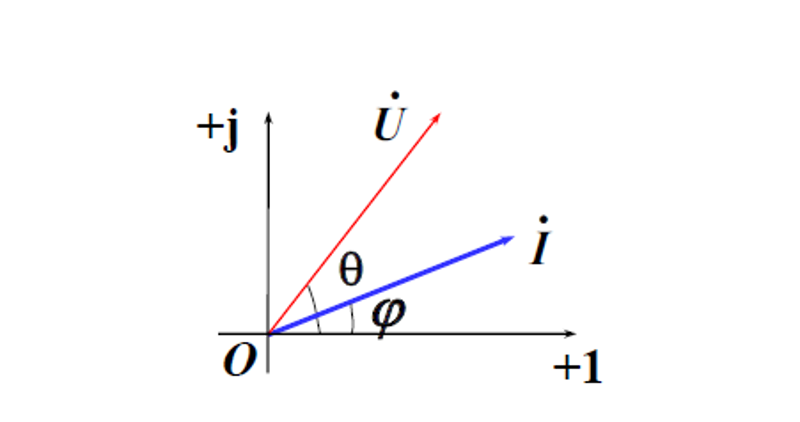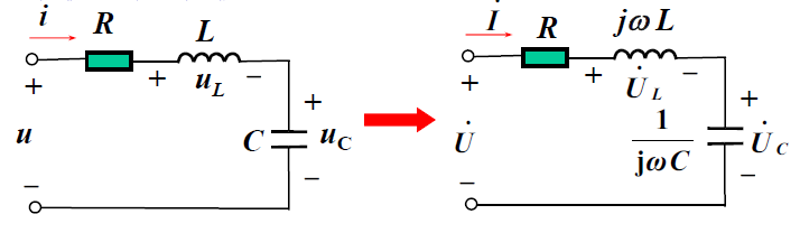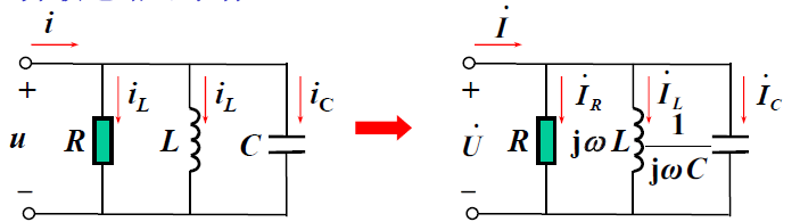相量法
复数
| 形式 |
表达式 |
| 代数形式 |
F=a+jb |
| 三角形式 |
F=∣F∣(cosθ+jsinθ) |
| 指数形式 |
F=∣F∣ejθ |
| 极坐标形式 |
$F=\lvert F\rvert \angle \theta $ |
其中∣F∣=a2+b2θ=arctanab, 欧拉公式:
eiθ=cosθ+isinθ=1∠θ
复数的运算:
原则:加减法用代数式,乘除法用指数或者极坐标式。
-
相等
-
加减(向量加减) A1±A2=(a1±a2)+j(b1±b2)
-
乘除(用指数形式来记忆)
F1⋅F2F2F1=∣F1∣⋅∣F1∣⋅ej(θ1+θ2)=∣F1⋅F2∣∠θ1+θ2=∣F2∣∣F1∣∠θ1−θ2
-
旋转(即模为1的乘除法)
例子:
220∠35∘+20+j5(17+j9)(4+j6)=180.2+j126.2+20.62∠14.04∘19.24∠27.9∘×7.211∠56.3∘=180.2+j126.2+6.728∠70.16∘=180.2+j126.2+2.28+j6.33=182.48+j132.53=225.5∠36∘
正弦量
在选定的参考方向下,电路中随时间按正弦规律变化的电压、电流等,称为正弦量。
i(t)=Imcos(ωt+φ)
要点:振幅(最大值),角频率(相角变化的速度),初相位。
相位差:φ12=φi1−φu2 各种叫法:
| 情况 |
叫法 |
| φ12<0 |
u提前i φ角, i滞后u φ角 |
| φ12=0 |
同相 |
| φ12>0 |
u滞后i φ角, i提前u φ角 |
| φ12=180∘ |
反相 |
| φ12=π/2 |
正交(称u提前i π/2角,或i滞后u π/2角 ) |
有效值
定义:瞬时值的平方在一个周期内积分的平均值再取平方根
IU=T1∫0Ti2(t)dt=T1∫0Tu2(t)dt
对于非正弦情况,因为如果一个函数是周期性的,且满足狄里赫利条件,那么它可以展开成一个收敛级数,即傅里叶级数。电工技术中所遇到的周期函数f(t)一般都能满足这个条件,因而可以分解为下列的傅里叶级数。根据傅立叶级数变换
f(t)=A0+k=1∑∞(Akcoskwt+Bksinkwt)
一个非正弦周期电流i可以分解为傅里叶级数:
i=I0+k=1∑∞Imksin(kωt+φk)
进而:
I=T1∫0T[I0+∑k=1∞Imksin(kωt+φk)]2dtT1∫0TI02dt=I02T1∫0TImk2sin2(kωt+φk)dt=(Imk2)2=Ik2T1∫0T2I0Imksin(kωt+φk)dt=0T1∫0T2Imksin(kωt+φk)Imqsin(qωt+φq)dt=0
最终得到非正弦周期电流i的有效值(电压同理):
I=I02+I22+I32+⋯Im2+⋯
向量表示
由于复数部分没有物理意义,所以可以用复数来表示正弦量。
i(t)=Imcos(ωt+φ)⇔A(t)=2Iej(ωt+φ)
因此可以用向量来表示正弦量如下
i(t)=2ICos(ωt+φ)→I˙=I∠φu(t)=2UCos(ωt+θ)→U˙=U∠θ
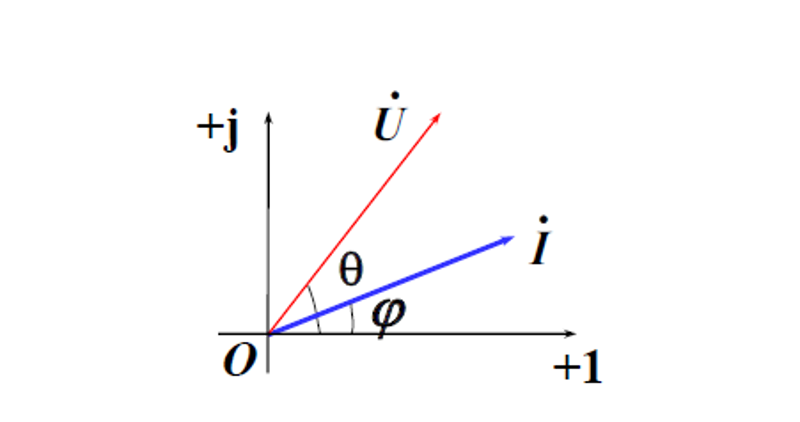
已知
i=141.4Cos(314t+30∘)Au=311.1Cos(314t−60∘)V
试用相量表示 i,u
i=100∠30∘AU˙=220∠−60∘V
同频率正弦量直接向量相加。
*三种基本电路元件伏安关系的相量形式
阻抗与导纳
(伏)阻抗定义
正弦激励下无源线性电路电压与电流的比值,代表限制电流的能力。
Z= def I˙U˙=I∠φiU∠φu=IU∠φu−φi=∣Z∣∠φZ=R+jX
其中∣Z∣=IU 称之为阻抗模,φZ=φu−φi称之为阻抗角,X称之为电抗。向量形式ZRX显而易见,再定义:
{R=Re[Z]=∣Z∣cosφZ电阻X=Im[Z]=∣Z∣sinφZ电抗
如果假设所在电路只有一个组件,则可以得到电阻、电容、电感的阻抗表达式如下
| 原件 |
(伏)阻抗ZR |
| R(电阻) |
R |
| L(感抗) |
jωL |
| C(容抗) |
1/jωC |
由上面的表达式可以得到:电阻阻抗不变;感抗与ω成正比,无穷大时开路;容抗与ω成反比,趋于零时其值最大(阻直流),无穷时其值趋于零(短路)。
由于电抗的存在,使电流、电压的相位不同,存在相位差。而电阻则不影响电路的相位,从下面的分析可见一二。
RLC串联电路的阻抗:
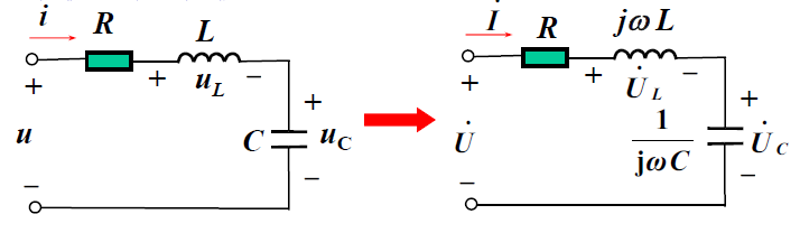
容易计算得到电抗值为:X=XL−XC=ωL−ωC1,因此,当电容电感取值不一样时,电压电流的相位关系有所不同:
⎩⎪⎨⎪⎧X>0,ωL>ωC1,φz>0, Z呈感性,电压超前电流X<0,ωL<ωC1,φz<0, Z呈容性,电压滞后电流X=0,ωL=ωC1,φZ=0, Z呈电阻性,谐振,电压、电流同相
经过上面的分析,可以看出阻抗的表达式由电阻分量与电抗分量组成:
Z(jω)=R(ω)+jX(ω)
*导纳的定义:
简而言之。导纳就是阻抗的倒数,导纳模,导纳角的定义不再赘述,
Y= def U˙I˙=U∠φuI∠φi=UI∠φi−φu=∣Y∣∠φy=G+jB
RLC并联电路的导纳:
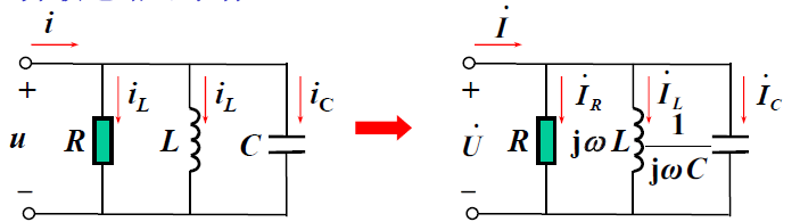
差不多,真的很像!简直一模一样!不写了,考试又不考,以后又不大用得上,知识,请原谅我的无情吧。
阻抗串联,求和方法与电阻一样。
导纳并联,各支路导纳直接加和。
正弦稳态电路的分析
电阻电路与正弦稳态电路相量法分析是极其相似的:
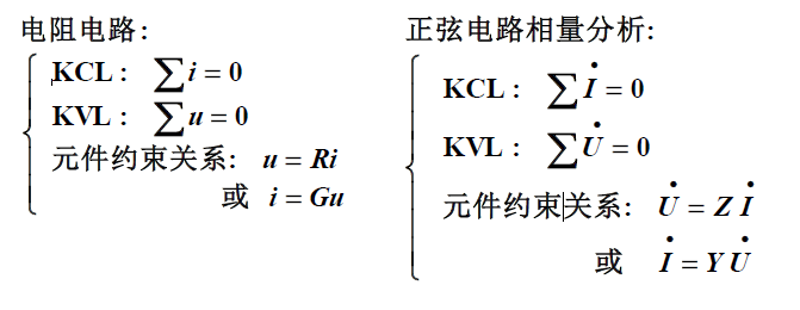
方法知道了,但总归还是多刷题:

正弦稳态电路的功率
有功(平均)功率
由上面i u 的表达式可以定义瞬时功率P:
p=ui=2Ucos(ωt+φu)⋅2Icos(ωt+φi)=2UIcos(ωt+φu)cos(ωt+φi)=UIcos(φu−φi)+UIcos(2ωt+φu+φi)=UIcosφ+UIcos(2ωt+φu+φi)
画成图像如下:
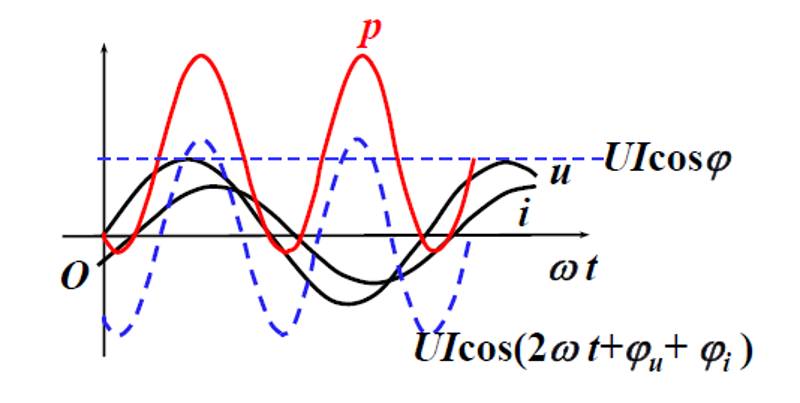
- p>0, 电路吸收功率,p<0,电路发出功率。
- p以2ω角频率变化。
但瞬时功率不断变化,没什么鸟用,我们可以用微积分思想来求其在一段时间内的平均功率,亦即在时间t内瞬时功率p的积分
P=T1∫0Tpdt=T1∫0TUI[cosφ+cos(2ωt+2φu+φi)]dt
P=UIcosφ(W)
称λ=cosφ 为功率因数,φ为功率因数角,对无源网络,为其等效阻抗的阻抗角。当cosφ=1为纯电阻电路,当cosφ=0为纯电抗电路。
无功功率
Q=UIsinφ(var)
Q>0,表示网络吸收无功功率;Q<0,表示网络发出无功功率。
Q 的大小反映网络与外电路交换功率的大小。是由储能元件L、C的性质决定的。
视在功率
S=UI(VA)
视在功率反映电气设备的容量。
S2=P2+Q2
φ=arctan(PQ)
φ代表电流与电压的相位差
| 原件&电路 |
φ=φu−φi |
| 电阻 |
0 |
| 电容 |
π/2 |
| 电感 |
−π/2 |
| RLC串联 |
φZ |
| RLC并联 |
φZ |
复功率
为了用向量来直接计算功率(天空总是很蓝,人们总是很懒)
U˙P=U∠φuI˙=I∠φi=UIcos(φu−φi)=UIRe[ej(φu−φi)]=Re(Uejφu⋅Ie−jφi)=Re[U˙⋅I˙∗]
Sˉ=U˙I˙∗
Sˉ=UI∠(φu−φi)=UI∠φ=S∠φ=UIcosφ+jUIsinφ=P+jQ
- 复功率守恒定理:在正弦稳态下,任一电路的所有支路吸收的复功率之和为零。
提高功率因数
功率因数过低时,设备不能充分利用,电流到了额定值,但功率还有容量没用; 当输出相同的有功功率时,线路上电流大I=P/(Ucosφ),线路压降损耗大。
解决方法:并联电容,提高功率因数(改进自身设备)。
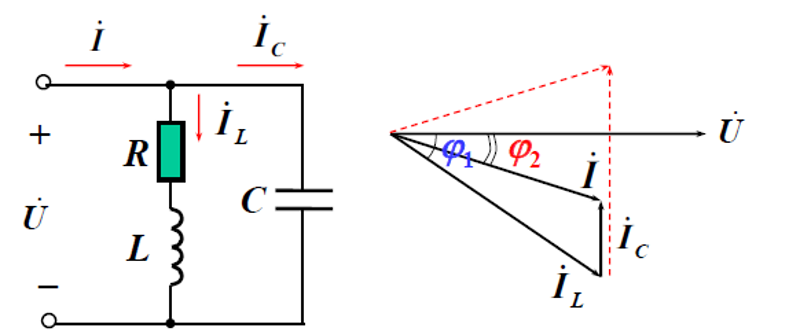
功率因数提高后,线路上电流减少,就可以带更多的负载,充分利用设备的能力。